Mahasiswa STIKOM Artha Buana yang baik, berikut saya sajikan Materi Aljabar Linier Persamaan Garis dan Titik Potong 2 Garis.
Persamaan Garis Melalui sebuah titik dengan Gradien tertentu
Persamaan garis dibentuk dari diketahuinya sebuah titik pada garis tersebut dan gradien yang menyertainya.
Misalnya :
 |
| Gambar 1. Sebuah Titik yg tepat pada garis |
Pada gambar 1, terlihat terdapat sebuah titik A(x1,y1) yang terdapat tepat pada garis tersebut.
Awal mula persamaan garis linear adalah :
y = mx + b, dimana y adalah variabel dependen terhadap x, m adalah gradien dan sebuah konstanta b.
jika diketahui titik tersebut pada A(x1,y1), maka persamaan garis linear di atas diubah menjadi :
y1 = mx1 + b, sehingga untuk mencari persamaan garisnya menjadi sebagai berikut :
y = mx + b .........................1
y1 = mx1 + b .........................2
Lakukan pengurangan antara y dan y1, sehingga menjadi :
y - y1 = m(x-x1) .................................................................................................................3
dan inilah yang dipakai sebagai acuan untuk menentukan persamaan garisnya.
Contoh :
A(6,1) dengan gradien 2, maka persamaan garisnya adalah :
 |
| Gambar 2. Persamaan Garis y=2x-11 |
y-y1 = m(x-x1)
y-1 = 2(x-6)
y = 2x -12 + 1
y = 2x -11
Sehingga dari persamaan y = 2x-11 dapat dilihat garisnya pada gambar 2.
Contoh lain lagi, misalkan diketahui sebuah titik pada sebuah garis adalah A(1,10) dengan gradien = 3, maka persamaan garisnya adalah :
y-y1 = m(x-x1)
 |
| Gambar 3. Persamaan garis y = 3x+7 |
y-10 = 3x - 3
y = 3x - 3 + 10
y = 3x +7 dari persamaan garis ini diperoleh garis seperti terlihat pada Gambar 3.
Persamaan garis yang melalui 2 buah titik
Bila diketahui 2 buah titik yang melalui sebuah garis, seperti pada Gambar 4.
 |
| Gambar 4. 2 buah titik pada garis |
Terlihat ada 2 buah titik, yaitu titik A(x1,y1) dan titik B(x2,y2). dan x1≠x2 dan y1≠y2, maka persamaan garisnya diperoleh dari :
Misalkan garis itu mempunyai persamaan
y = ax + b ...............................................(1)
Titik (x1, y1)
pada garis itu, berarti
y1 = ax1 + b................................................(2)
Titik (x2, y2)
pada garis itu, berarti
y2 = ax2 + b
...............................................(3)
(1)–(2) menghasilkan y – y1
= a(x–x1)........(4)
(3)-(2) menghasilkan y2 – y1 = a(x2–x1)….(5)
(4)
: (5) menghasilkan :
 |
| Gambar 6. Rumus baru untuk Persamaan garis dg 2 titik |
Contoh :
Diketahui 2 buah titik, yaitu A (-3, -4) dan B (5, -1) Carilah persamaan garisnya ?
Jawab :
8(y+4) = 3(x+3)
8y+32 = 3x+9
8y = 3x + 9 -32
8y = 3x -23
Sehingga dari persamaan garis tersebut diperoleh grafik seperti terlihat pada gambar 6.
 |
| Gambar 6. Persamaan Garis y=(3x-23)/8 |
Titik Potong 2 Garis
Bila diketahui 2 buah persamaan garis, yaitu :
2x-3y =14 dan x = 5y, maka untuk mencari titik potong dari kedua garis tersebut digunakan metode subtitusi (mengganti sebuah nilai dengan nilai yang sudah ada). Tujuan dari subtitusi ini adalah agar diperoleh sebuah variabel saja dalam persamaan tersebut. Terlihat bahwa x sudah diketahui isinya, yaitu 5y, maka kalau disubtitusikan ke rumus yang pertama (2x-3y=14), menjadi :
2(5y) - 3y = 14
10y - 3y = 14
7 y = 14
y = 14/7 = 2
Kalau y=2, maka x = 5y --> 5*2 = 10.
Sehingga titik potong kedua garis tersebut adalah pada titik (10,2)
Grafiknya bisa dilihat pada gambar 7.
Pada contoh lain, dimana variabel tidak ada yang tunggal, maka perlu metode eliminasi, yaitu dengan cara mengalikan dengan sebuah angka sehingga ada variabel yang mempunyai koefisien yang sama.
y = 14/7 = 2
Kalau y=2, maka x = 5y --> 5*2 = 10.
Sehingga titik potong kedua garis tersebut adalah pada titik (10,2)
Grafiknya bisa dilihat pada gambar 7.
 |
| Gambar 7. Titik potong 2 Garis |
Pada contoh lain, dimana variabel tidak ada yang tunggal, maka perlu metode eliminasi, yaitu dengan cara mengalikan dengan sebuah angka sehingga ada variabel yang mempunyai koefisien yang sama.
Misalkan :
2x + 5y = 6 dan 3x - 7y = 5, maka masing-masing dikalikan dengan 3 dan 2 menjadi :
2x + 5y = 6 x 3
3x - 7y = 5 x 2
menjadi :
6x + 15y = 18
6x -14y = 10
. . -
0 29y = 8
y = 8/29
Kemudian mensubtitusikan nilai y yang didapat kedalam rumus pertama atau ke dua.
2x + 5y = 6
2x + 5(8/29) = 6
2x + 40/29 = 6
2x = 6 - 40/29
x = (6-40/29)/2 Sehingga titik potongnya di (8/29 , (6-40/29)/2)
Grafiknya seperti terlihat pada gambar 8.
 |
| Gambar 8. Titik Potong 2 Garis dg Variabel belum final |
Materi Presentasi bisa didownload disini
Dan yang dari Slideshare :
Aljabar Linear Pertemuan 1-1
Aljabar Linear Pertemuan 1-2
Dan yang dari Slideshare :
Aljabar Linear Pertemuan 1-1
Aljabar Linear Pertemuan 1-2

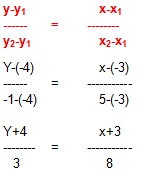
pak bagaimana cara mencari persamaan garis yang baru dari 2 persamaan : a. 2x+y=6 dan b. x+2y=4??
ReplyDeleteMencari persamaan garis yg baru dari 2 persamaan ? Bukan titik potong dari 2 garis bu ? Karena sepengetahuan saya tidak ada persamaan garis baru yg dibentuk dari 2 persamaan garis.
ReplyDeleteKalau titik potong, maka :
2x + y = 6
x + 2y = 4 x2
2x + y = 6
2x + 4y = 8
------------- -
-3y = -2
-y = -2/3
y = 2/3
x + 2y = 4
x + 2*2/3 = 4
x = 4 - 4/3
Sehingga titik potongnya di ((4-4/3),(2/3))
Mantapp Pak..
ReplyDeleteMas Fari Madyan : terima kasih mas, ini hanya sharing sedikit yang saya tahu saja
ReplyDeleteTerimakasih kaaak! Sangat membantu!
ReplyDelete#G Noire : sama-sama, hanya membantu sedikit.........
ReplyDeletePak, bagaimana contoh soal tentang membuat persamaan garis yang melalui titik A dan tegak lurus dengan titik B dan C dan mencari titik potong (angka bulat) bagaimana ya pak? Tolong saya pak. Terimakasih pak.
ReplyDeleteMenjawab pertanyaan saudara Anonymous, mudah-mudahan saya punya solusi.
ReplyDeleteTolong dicek pada link berikut : http://haidaroh.blogspot.com/2014/09/persamaan-garis-saling-tegak-lurus.html
Terima kasih
Pak bantu kerjain tugas aku dong...
ReplyDeleteMenentukan persamaan garis melalui titik potong garis 3x+4y=12 dan x-4y=0
Untuk Novhy : mencari titik potong dari 2 garis ya ( garis 3x+4y=12 dan garis x-4y=0), kalau iya, maka jawabannya cukup sederhana, yaitu dengan menggunakn metode eliminasi salah satu variabelnya.
ReplyDelete3x+ 4y = 12
x - 4y = 0
------------------ +
4x = 12
x = 12/4 = 3; sehingga y adalah :
x - 4y = 0
3 - 4y = 0
3 = 4y.
y = 3/4. Jadi titik potong kedua garis tersebut adalah di titik (3, 3/4)
Mudah-mudahan bisa membantu.
Pak tolong bantu saya, cari tipot dari 2 persamaan ini x+2y+5=0 dan 2x+3y+15=0
ReplyDeleteUntuk saudara/i nyanyats, mohon maaf saya terlambat membalas karena kesibukan saya. Untuk itu inilah jawaban yang mungkin saya bisa berikan :
ReplyDeleteTipot x+2y+5=0 dan 2x+3y+15=0, kita gunakan metode eliminasi, yaitu salah satu variabelnya kita nol kan. Misalnya viabel x akan kita hilangkan, dengan cara :
x+2y=-5 --> *2 menjadi 2x+4y=-10
2x+3y=-15
Kemudian kita kurangkan kedua persamaan tersebut (kurangkan ke bawah --> persamaan 1 dikurangi persamaan 2), dan hasilnya adalah : 0 +1y = 5 sehingga y=5.
Selanjutnya subtitusi y untuk persamaan 1 atau 2 (pilih salah satu), misalnya kita pilih persamaan 1, yaitu x+2y+5=0, gantilah y dengan nilai 5 menjadi --> x + 2*5 + 5 = 0 --> x + 10 + 5 = 0 --> x = -10 - 5 ==> x = -15
Sehingga disimpulkan bahwa titik potong kedua persamaan tersebut adalah di titik (-15,5)
Demikian jawaban saya, semoga bermanfaat.
pak tolong bantu kerjain tugas saya dong..
ReplyDeletePersamaan garis yang melalui titik potong garis dgn persamaan 2x + 5y = 1 dan x - 3y = -5 serta tegak lurus pd garis dengan persamaan 2x - y + 5 = 0 adalah ...
Untuk adik Iklimah Camia, mohon maaf terlambat menjawab karena kesibukan.
ReplyDeleteJawaban yang menurut saya pas dengan pertanyaan adik, dapat dilihat pada link berikut :
http://haidaroh.blogspot.com/2015/01/garis-tegak-lurus-pada-titik-potong-2.html
Terima kasih
terimakasih....................................... sangat membantu..............................
ReplyDeleteBuat Fitri Alifa : sama-sama
ReplyDeletePak gimana kalo diketahui persamaan 2 garis ax+3y=5 dan 2x+by=3 memiliki titik potong lebih dari 2, maka a.b adalah...
ReplyDeletekalau 2 persamaan garis dan persamaan tersebut linier, kalau berpotongan PASTI hanya punya 1 titik potong saja (karena tidak mungkin garis itu melingkar balik). Jadi sangat tidak mungkin untuk terjadi titik potongnya lebih dari 1.
Deletepak/bu klu misalnya soalnya itu:
ReplyDeletepersamaa garis yg melalui titik (x,y) dan titik potong antara garis y=mx+c dan y=x+c itu caranya yg mana?
terima kasih. mohon segera di jawab
pak/bu kalau untuk, persamaan garis yang melalui titik (2,5) dan titik potong antara garis y=2x+6 dengan y=-x+3,itu pakai rumus yg mana ya?
ReplyDeleteterima kasih mohon segera di jawab
Untuk saudari Irma Komariyah, berikut link jawaban saya. Tetapi mungkin tidak bisa memuaskan.
ReplyDeletehaidaroh blog: Menjawab Persamaan Garis dan TIPOT
http://haidaroh.blogspot.co.id/2016/03/menjawab-persamaan-garis-dan-tipot.html
sangat membantu pak atas blogspot nya
ReplyDeleteGunawan Paraduan : hanya sedikit share saja, mudah-mudahan bisa membantu
ReplyDeletePak tolong bantu saya.
ReplyDeleteTentukan persamaan garis dan grafik bila diketahui dua titik: A(-6,-4) dan B(10,8).
Terimakasih
Terima kasih atas kunjungannya. Berikut jawaban yg saya coba berikan, mudah2an membantu.
DeleteTitik Pertama adalah A(-6,-4) dan titik Kedua adalah B(10,8). Sehingga dapat dimisalkan bahwa : A(X1,Y1) dan B(X2,Y2). Maka :
(Y-Y1)/(Y2-Y1)=(X-X1)/(X2-X1)
(Y-(-4))/(8-(-4))=(X-(-6))/(10-(-6))
(Y+4)/(8+4)=(X+6)/(10+6)
(Y+4)/12 = (X+6)/16; Lakukan perkalian silang menjadi :
12(X+6)=16(Y+4);
12X+72=16Y+64; pindahkan yg bervariabel menjadi 1 tempat dan yg tidak bervariabel jadi satu tempat juga menjadi :
12X-16Y=64-72;
12X-16Y=-8 ; perlu dibuat menjadi sederhana menjadi :
12X+8=16Y; sehingga Y = (12X+8)/16;
INI ADALAH PERSAMAAN GARISNYA. Tinggal membuat data permisalan dengan nilai X mulai dari -5 sampai dengan 10, maka y tinggal mencari (pakai excel saja).
Untuk grafiknya bisa dilihat pada link ini : http://www.4shared.com/photo/BJ8fgdVdce/Grafik.html
pak saya mau tanya.
ReplyDeletetentukan bentuk hubungan 2 garis lurus dari
a) persamaan 2x + 6y - 4 = 0 dan -3y + y - 4 = 0
b) persamaan 2x + y + 4 = 0 dan 2x + 6y - 4 = 0
Mohon maaf adik Monika Khonik. Saya baru bisa balas.
Deletesaya akan berusaha mamahami yg menjadi pertanyaan kamu.
a. Bahwa kedua persamaan tersebut saya asumsikan berpotongan, maka saya mencarinya dengan pendekatan perpotongan garis.
2x+6y-4=0
-3x+y-4=0, ubahlah masing-masing menjadi :
2x+6y=4
-3x+y=4
Lakukan eliminasi (menghilangkan salah satu variabel, misalnya x) dengan cara mengalikan masing2 persamaan sehingga koefisien x menjadi sama)
2x+6y=4 kali 3
-3x+y=4 kali 2, menjadi :
6x+18y=12
-6x+2y=8, kemudian jumlahkan (kadang2 kurangkan), menjadi :
--------- +
0 + 20y=20
y=20/20 = 1, sehingga y=1
Subtitusikan nilai y dengan y dan masukkan kedalam salah satu persamaan :
2x+6y=4 --> 2x+6*1=4
2x+6=4 --> 2x = 4-6 --> 2x=-2 --> x=-2/2 --> x=-1
Karena nilai x dan y sudah diketemukan, maka kedua garis tersebut berpotongan di titik (-1,1).
b. 2x+y+4=0 dan 2x+6y-4=0, diubah menjadi :
2x+ y=-4
2x+6y=4, lakukan eliminasi salah satu variabelnya (x yg dieliminasi karena koefisien sudah sama), menjadi :
2x+ y=-4
2x+6y= 4
-------- -
0 -5y=-8
y=-8/-5 --> y=8/5 --> y=1.6
Subtitusikan nilai y dengan 1.6 dan masukkan kedalam salah satu persamaan :
2x+y=-4
2x+1.6=-4
2x=-4-1.6
2x=-5.6
x=-5.6/2 --> x=-2.8
Sehingga dapat disimpulkan bahwa kedua persamaan tersebut berpotongan dititik (-2.8,1.6).
Grafiknya dapat diunduh pada link berikut :
https://www.4shared.com/photo/hbDKBGPyce/aaa.html
Demikian terima kasih
Permisi saya mau tanya tentang soal ini
ReplyDeleteTentykan titik potong garis
Y=-2q+2 dan y= 1/2q + 25
Gimana ya penyelesaian nya
Untuk mas Herry Permana. Mudah2an saya bisa menjawab.
DeleteDiketahui persamaan 1 dan 2 adalah : Y=-2q+2 dan Y=1/2q+25
Ditanyakan : titik potong kedua persamaan tersebut dititik mana ?
Jawab :
Buat eliminasi terlebih dulu (dg menghilangkan salat satu variabel, misalnya q) dg cara :
y= -2q+2 --> y+ 2q = 2
y=1/2q+25 --> y-1/2q = 25 x 4
==> y + 2q = 2
==> 4y -2q = 100
------------- +
5y = 102
y = 102/5 = 20,4
kemudian masukkan (subtitusi) nilai q yg diperoleh tersebut kedalam salah satu persamaan garisnya. Misalnya saya pakai y=-2q+2, maka :
20,4=-2q+2 ==> 20,4 - 2 = -2q ==> 18.4/-2 = q
q = -9.2
Sehingga titik potong kedua garis tersebut ketemu di (-9.2,20.4)
Untuk grafiknya bisa dilihat pada link https://www.4shared.com/photo/jZwWdHHIba/Untitled.html
Pak tlong bntu tugas saya.
ReplyDeleteTentukan fungsi/persamaan garis apabila melalui titik E(-3,-2) ; C(4,-2). Mkasih sebelumnya pak.
Untuk adik Jijah Aritra, mudah2an saya bisa menjawab.
DeleteKarena sudah diketahui 2 titik, maka rumus yang dipakai adalah : (y-y1)/(y2-y1)=(x-x1)/(x2-x1), sehingga :
(y-(-2))/(-2-(-2))=(x-(-3))/(4-(-3))
==>(y+2)/0=(x+3)/7
==>7(y+2)=0(x+3)
==>(7y+14)=0
==>7y+14=0
==>7y=-14
==>y=-14/7
==>y=-2
Sehingga persamaan garisnya adalah y=-2.
Artinya bahwa semua titik-titik pada y=-2 adalah anggota persamaan garis tersebut berapapun nilai x nya.
Assalamu'alaikum pak. Mo nanya.
ReplyDeletePersamaan garis yg tegak lurus 2x + y = 1 & melalui titik potong garis x = 4y + 4 dengan y=7. Tolong y pak..
Wa'alaikum salam warahmatulahi wabarakatuhu.
DeleteMohon dibaca tulisan saya yang lain di Label : Ahmad Haidaroh - Aljabar Linear
Ada beberapa persoalan yang hampir sama. Bisa dicoba untuk soal punya kamu.
Pak bantu saya , tentukan persamaan garis yang tegak lurus dgn garis 2y-x-6=0 dan melalui titik potong garis 2y-x-6=0 dan garis y=4. Trmksh
ReplyDeleteMohon dibaca tulisan saya yang lain di Label : Ahmad Haidaroh - Aljabar Linear
DeleteAda beberapa persoalan yang hampir sama. Bisa dicoba untuk soal punya kamu.
pak tolong dibantu, tentukan persamaan garis yang melalui titik (1,-3) dan titik potong garis y= 2x dengan y= 5x -4. cara ngerjainnya gimana pak?
ReplyDeleteAnda baca di
Deletehttps://haidaroh.blogspot.co.id/2016/03/menjawab-persamaan-garis-dan-tipot.html