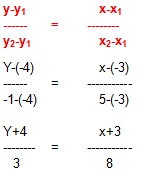Mahasiswa STIKOM Artha Buana yang baik, berikut saya sajikan Materi Aljabar Linier Persamaan Garis dan Titik Potong 2 Garis.
Persamaan Garis Melalui sebuah titik dengan Gradien tertentu
Persamaan garis dibentuk dari diketahuinya sebuah titik pada garis tersebut dan gradien yang menyertainya.
Misalnya :
 |
| Gambar 1. Sebuah Titik yg tepat pada garis |
Pada gambar 1, terlihat terdapat sebuah titik A(x1,y1) yang terdapat tepat pada garis tersebut.
Awal mula persamaan garis linear adalah :
y = mx + b, dimana y adalah variabel dependen terhadap x, m adalah gradien dan sebuah konstanta b.
jika diketahui titik tersebut pada A(x1,y1), maka persamaan garis linear di atas diubah menjadi :
y1 = mx1 + b, sehingga untuk mencari persamaan garisnya menjadi sebagai berikut :
y = mx + b .........................1
y1 = mx1 + b .........................2
Lakukan pengurangan antara y dan y1, sehingga menjadi :
y - y1 = m(x-x1) .................................................................................................................3
dan inilah yang dipakai sebagai acuan untuk menentukan persamaan garisnya.
Contoh :
A(6,1) dengan gradien 2, maka persamaan garisnya adalah :
 |
| Gambar 2. Persamaan Garis y=2x-11 |
y-y1 = m(x-x1)
y-1 = 2(x-6)
y = 2x -12 + 1
y = 2x -11
Sehingga dari persamaan y = 2x-11 dapat dilihat garisnya pada gambar 2.
Contoh lain lagi, misalkan diketahui sebuah titik pada sebuah garis adalah A(1,10) dengan gradien = 3, maka persamaan garisnya adalah :
y-y1 = m(x-x1)
 |
| Gambar 3. Persamaan garis y = 3x+7 |
y-10 = 3(x-1)
y-10 = 3x - 3
y = 3x - 3 + 10
y = 3x +7 dari persamaan garis ini diperoleh garis seperti terlihat pada Gambar 3.
Persamaan garis yang melalui 2 buah titik
Bila diketahui 2 buah titik yang melalui sebuah garis, seperti pada Gambar 4.
 |
| Gambar 4. 2 buah titik pada garis |
Terlihat ada 2 buah titik, yaitu titik A(x1,y1) dan titik B(x2,y2). dan x1≠x2 dan y1≠y2, maka persamaan garisnya diperoleh dari :
Misalkan garis itu mempunyai persamaan
y = ax + b ...............................................(1)
Titik (x1, y1)
pada garis itu, berarti
y1 = ax1 + b................................................(2)
Titik (x2, y2)
pada garis itu, berarti
y2 = ax2 + b
...............................................(3)
(1)–(2) menghasilkan y – y1
= a(x–x1)........(4)
(3)-(2) menghasilkan y2 – y1 = a(x2–x1)….(5)
(4)
: (5) menghasilkan :
 |
| Gambar 6. Rumus baru untuk Persamaan garis dg 2 titik |
Contoh :
Diketahui 2 buah titik, yaitu A (-3, -4) dan B (5, -1) Carilah persamaan garisnya ?
Jawab :
8(y+4) = 3(x+3)
8y+32 = 3x+9
8y = 3x + 9 -32
8y = 3x -23
Sehingga dari persamaan garis tersebut diperoleh grafik seperti terlihat pada gambar 6.
 |
| Gambar 6. Persamaan Garis y=(3x-23)/8 |
Titik Potong 2 Garis
Bila diketahui 2 buah persamaan garis, yaitu :
2x-3y =14 dan x = 5y, maka untuk mencari titik potong dari kedua garis tersebut digunakan metode subtitusi (mengganti sebuah nilai dengan nilai yang sudah ada). Tujuan dari subtitusi ini adalah agar diperoleh sebuah variabel saja dalam persamaan tersebut. Terlihat bahwa x sudah diketahui isinya, yaitu 5y, maka kalau disubtitusikan ke rumus yang pertama (2x-3y=14), menjadi :
2(5y) - 3y = 14
10y - 3y = 14
7 y = 14
y = 14/7 = 2
Kalau y=2, maka
x = 5y --> 5*2 = 10.
Sehingga titik potong kedua garis tersebut adalah pada titik
(10,2)
Grafiknya bisa dilihat pada gambar 7.
 |
| Gambar 7. Titik potong 2 Garis |
Pada contoh lain, dimana variabel tidak ada yang tunggal, maka perlu metode eliminasi, yaitu dengan cara mengalikan dengan sebuah angka sehingga ada variabel yang mempunyai koefisien yang sama.
Misalkan :
2x + 5y = 6 dan 3x - 7y = 5, maka masing-masing dikalikan dengan 3 dan 2 menjadi :
2x + 5y = 6 x 3
3x - 7y = 5 x 2
menjadi :
6x + 15y = 18
6x -14y = 10
. . -
0 29y = 8
y = 8/29
Kemudian mensubtitusikan nilai y yang didapat kedalam rumus pertama atau ke dua.
2x + 5y = 6
2x + 5(8/29) = 6
2x + 40/29 = 6
2x = 6 - 40/29
x = (6-40/29)/2 Sehingga titik potongnya di (8/29 , (6-40/29)/2)
Grafiknya seperti terlihat pada gambar 8.
 |
| Gambar 8. Titik Potong 2 Garis dg Variabel belum final |