Definisi
Secara umum konvolusi didefinisikan sebagai cara untuk mengkombinasikan dua buah deret angka yang menghasilkan deret angka yang ketiga.
Secara matematis, konvolusi adalah integral yang mencerminkan jumlah lingkupan dari sebuah fungsi a yang digeser atas fungsi b sehingga menghasilkan fungsi c. Konvolusi dilambangkan dengan asterisk (*).
Sehingga, a*b = c; berarti fungsi a dikonvolusikan dengan fungsi b menghasilkan fungsi c.
Dan bila secara diskrit, maka rumusnya menjadi :
a = [1, 2, 3] dan b = [4,5,6], dimana poros untuk a berada di 1 dan poros untuk b berada di 4 maka a * b :
Fungsi b : 4 5 6
Fungsi a dibalik : 3 2 1 ........................ (4*1) = 4
3 2 1 ....................(4*2)+(5*1) = 13
3 2 1 ...............(4*3)+(5*2)+(6*1)=28
3 2 1 ..........(5*3)+(6*2) = 27
3 2 1 .....(6*3) = 18
Sehingga a*b = [4, 13, 28, 27, 18]
Konvolusi dikawasan waktu (time domain) ekuivalen dengan perkalian dikawasan frekuensi dan sebaliknya konvolusi dikawasan frekuensi ekuivalen dengan perkalian dikawasan waktu [Bracewell, 1965]
- Rumus konvolusi muncul dari adanya sifat linieritas dan invarian waktu pada sistem. Sebagai konsekwensinya, respon sistem terhadap setiap sinyal masukan yang berubah-ubah dapat dinyatakan dari segi respon cuplikan unit sistem.
- Misal dipunyai sinyal x[n] yang berubah-ubah, maka x[n] dapat didekomposisi menjadi jumlahan bobot (skala) deret cuplikan unit yang digeser (impuls)
- Contoh. Perhatikan kasus barisan berhingga berikut :
- Pisahkan y[n] menjadi jumlah bobot deret impuls !
Konvolusi menggabungkan tiga buah sinyal --> sinyal masukan, sinyal keluaran, dan respon impuls. Konvolusi adalah cara matematik untuk mengkombinasikan dua buah sinyal menjadi sinyal dalam bentuk lain.
Notasi Konvolusi
y[n]= x[n] * h[n] bersifat komutatif, sehingga bisa juga menjadi y[n]= h[n] * x[n]
Langkah-langkah Konvolusi
- Pencerminan (folding). Cerminkan h[k] pada k=0 untuk memperoleh h[-k]
- Pergeseran (shifting). Geser h[-k] dengan n0 ke kanan (kiri) jika n0 positif (negatif) untuk memperoleh h[n0-k]
- Perkalian (multiplication). Kalikan x[k] dengan h[n0-k] untuk memperoleh produk
- Penjumlahan (summation). Jumlahkan seluruh nilai deret produk Vn0[k] untuk memperoleh nilai pada waktu n=n0
Contoh Konvolusi dengan cara yang lain adalah sebagai berikut :
Respon impuls dari suatu sistem LTI (Linier Time Invariant) adalah :
h[n]={1, 2, 1,-1}
Respon impuls dari suatu sistem LTI (Linier Time Invariant) adalah :
h[n]={1, 2, 1,-1}
Tentukan respon sistem terhadap sinyal masukan :
x[n]={1, 2, 3,1}
Penyelesaian :
Untuk menjawab permasalahan diatas dapat dilakukan Dengan 2 cara --> secara grafik dan secara analitik
1. Secara Grafik
 |
| Gambar 1. Penyelesaian Konvolusi dengan grafik |
2. Secara Analitik
 |
| Gambar 2. Penyelesaian Konvolusi dengan cara analitik |
Proses pemilteran dengan konvolusi pada sinyal noise
 |
| Gambar 3. Pemilteran dengan konvolusi pada noise |
Contoh Lain Konvolusi
Contoh operasi konvolusi pada data 1 dimensi :
Didefinisikan ⊗ adalah operasi konvolusi, maka :
Caranya :
{0,1,2,3,2,1,0} digeser dulu ke kanan menyamakan porosnya, sehingga menjadi : {0,0,1,2,3,2,1}
{0,0,1,2,3,2,1}
{1,3,1} ........................... 0*1+0*3+1*1 = 1
{1,3,1} ........................ 0*1+1*3+2*1 = 5
{1,3,1} ..................... 1*1+2*3+3*1 = 10
{1,3,1}................... 2*1+3*3+2*1 = 13
{1,3,1} ............... 3*1+2*3+1*1 = 10
{1,3,1} ............ 2*1+1*3+0*1 = 5
{1,3,1} ......... 1*1+0*3+0*3 = 1
Sehingga grafikyang diperoleh dari kedua persamaan f(x) dan h(x) tersebut adalah :
Penggalan program untuk konvolusi ini adalah sebagai berikut :
#!/usr/bin/perl
@a=(1,2,3);
@b=(4,5,6);
$la=@a; #length a
$lb=@b; #length b
$lab=$la+$lb-1; #length of result
for ( $i = 0; $i < $lab; $i++ )
{
$k=$i;
$y[$i]= 0;
for ( $j = 0; $j < $lb; $j++ ) #length b
{
if ($k>=0 && $k<$lab)
{
$y[$i] = $y[$i] + ($a[$k]*$b[$j]);
$k=$k-1;
}
}
print $y[$i], "\n";
}
Thank's.
Contoh operasi konvolusi pada data 1 dimensi :
- f(x) = {0,1,2,3,2,1,0}
- g(x) = {1,3,1}
dimana pusat dari f(x) adalah 0 dan pusat dari g(x) adalah 3. g(x) dicerminkan dulu dengan poros cermin di angka 3, maka hasilnya juga tetap{1,3,1}.
Didefinisikan ⊗ adalah operasi konvolusi, maka :
- h(x) = f(x) ⊗ g(x) = {1,5,10,13,10,5,1}
Caranya :
{0,1,2,3,2,1,0} digeser dulu ke kanan menyamakan porosnya, sehingga menjadi : {0,0,1,2,3,2,1}
{0,0,1,2,3,2,1}
{1,3,1} ........................... 0*1+0*3+1*1 = 1
{1,3,1} ........................ 0*1+1*3+2*1 = 5
{1,3,1} ..................... 1*1+2*3+3*1 = 10
{1,3,1}................... 2*1+3*3+2*1 = 13
{1,3,1} ............... 3*1+2*3+1*1 = 10
{1,3,1} ............ 2*1+1*3+0*1 = 5
{1,3,1} ......... 1*1+0*3+0*3 = 1
Sehingga grafikyang diperoleh dari kedua persamaan f(x) dan h(x) tersebut adalah :
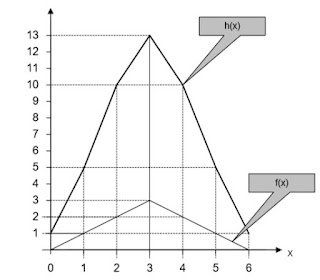 |
| Gambar 4. Grafik hasil Konvolusi |
Penggalan program untuk konvolusi ini adalah sebagai berikut :
#!/usr/bin/perl
@a=(1,2,3);
@b=(4,5,6);
$la=@a; #length a
$lb=@b; #length b
$lab=$la+$lb-1; #length of result
for ( $i = 0; $i < $lab; $i++ )
{
$k=$i;
$y[$i]= 0;
for ( $j = 0; $j < $lb; $j++ ) #length b
{
if ($k>=0 && $k<$lab)
{
$y[$i] = $y[$i] + ($a[$k]*$b[$j]);
$k=$k-1;
}
}
print $y[$i], "\n";
}
Thank's.













